04 - MATLAB, continued
04 - MATLAB, continued
Displaying data
By default, if no semicolon (;) is placed after a
command, MATLAB will display the operation result and display name of
the variable, to which it was assigned:
1 + 1ans =
2
Usually, the operation output is silenced, and results are displayed
in a desired format. The easiest way to do it is using the
disp() command:
a = [1 5 3; 63 22.6 2; 12.9 5 3];
disp('Matrix:');
disp(a);
disp('Single element:');
disp(a(3, 2));
disp('First row:');
disp(a(1, :));Matrix:
1.0000 5.0000 3.0000
63.0000 22.6000 2.0000
12.9000 5.0000 3.0000Single element:
5First row:
1 5 3
Conditional
expressions if .. elseif .. else .. end
Conditional expressions allow execution of parts of code, if a
specific condition has been met. In MATLAB, an exemplary if
use can be as follows:
if x < 0
disp('Negative value')
elseif x == 0
disp('Zero')
elseif x == 1
disp('One')
else
disp('More than zero but not one')
endEach if statement has to be closed with an
end keyword. All elseif and else
statements are optional and depend on particular use case. Each
elseif/else clause is executed only if all the
previous conditions were not met.
The following comparison operators are available <,
<=, >, >=,
== (equal), ~= (not equal). More complex
conditions can be assembled using logical operators
&& (and), || (or), ~
(not).
🔨 🔥 Assignment 🔥 🔨
Write a script, which will:
- Generate a single random number using
rand()command. - Using a conditional statement, display a proper message:
- “Too little!” - if generated number is smaller than 0.25.
- “Perfect!” - if generated number is greater or equal 0.25 and smaller or equal 0.75.
- “Too much!” - if generated number is greater than 0.75.
Loops: for .. end
In MATLAB, for loop can iterate over elements of a
vector:
for odd = [1:2:10] % definition of elements to iterate
disp(odd) % each element is assigned to a specified variable
end
even = [2:2:10];
for e = even % iteration can be done over an existing element
disp(e)
end1 3 5 7 9
2 4 6 8 10
🔨 🔥 Assignment 🔥 🔨
- Generate a random matrix of size 10x6 (rows x columns) and assign to a variable.
- Using a
forloop, add a number from 1 to 6 to each column, respectively.
Logical operations on vectors and matrices
Comparison operators
An important feature of MATLAB is ability to do logical operations on whole vectors (similar to mathematical operations during previus class), avoiding the need of using a loop.
A vector or matrix can be compared with a scalar or another vector of
matrix of the same dimensions, resulting in a boolean vector with
true/false (0/1) values:
x = [0.3188 0.4242 0.5079 0.0855 0.2625 0.8010 0.0292];
y = x < 0.5;
disp('Values smaller than 0.5 at:');
disp(y);
a = [1 2 3; 4 5 6; 7 8 9];
b = [2 3 3; 4 3 8; 1 8 3];
disp('Matrices are not equal at:');
disp(a ~= b);Values smaller than 0.5 at:
1 1 0 1 1 0 1Matrices are not equal at:
1 1 0
0 1 1
1 0 1
The boolean matrix can be used as an index to pick elements which satisfy a specific condition:
x = [0.3188 0.4242 0.5079 0.0855 0.2625 0.8010 0.0292];
disp('Values smaller than 0.5:');
disp(x(x < 0.5));Values smaller than 0.5:
0.3188 0.4242 0.0855 0.2625 0.0292
Logical operators
Complex conditions using boolean matrices can be done using logical
operators: & (and), | (or), ~
(not):
x = [0.3188 0.4242 0.5079 0.0855 0.2625 0.8010 0.0292];
x_logic = (x > 0.25) & (x < 0.75);
disp('Numbers higher than 0.25 and lower than 0.75:');
disp(x(x_logic));Numbers higher than 0.25 and lower than 0.75:
0.3188 0.4242 0.5079 0.2625
This way, loops can be avoided. An operation of picking values which meet a condition written with a loop:
x_vector = [0.3188 0.4242 0.5079 0.0855 0.2625 0.8010 0.0292];
disp('Numbers larger than 0.4:')
for x = x_vector
if x > 0.4
disp(x)
end
endCan be simplified:
x_vector = [0.3188 0.4242 0.5079 0.0855 0.2625 0.8010 0.0292];
disp('Numbers larger than 0.4:')
disp(x_vector(x_vector > 0.4)')Value assignment can also be done this way:
x = [0.3188 0.4242 0.5079 0.0855 0.2625 0.8010 0.0292];
disp(x)
x(x < 0.6) = -1;
disp(x)🔨 🔥 Assignment 🔥 🔨
Create an
xvector containing values in tange <-3, 3>, with 0.01 step.Calculate values of a given polynomial function for above
xvalues.
- Calculate:
- Boolean vector specifying where function value is greater than 50.
- Boolean vector specifying where function value is smaller than 20.
- Display in a single graph:
- Whole polynomial in range <-3, 3> with continuous blue line.
- With red circles (without connecting line) parts of polynomial where values are greater than 50.
- With green crosses (without connecting line) parts of polynomial where values are smaller than 20.
Reading CSV files
CSV - Comma Separated Value is a popular file format for saving tabular data, in which elements are divided with a specific seperator (usually, as name implies, a comma), and a new line means the beginning of a new row:
0.48,400,3.2,2.90367
1,2,3,4
73.2,75.2,723,222.3
MATLAB has a built-in csvread() function for reading a
CSV file contents into a numeric matrix:
data = csvread('sample.csv');
disp(data)0.4800 400. 3.2000 2.9037
1.0000 2.0000 3.0000 4.0000
73.2000 75.2000 723.0000 222.3000
Exporting graphs
Exporting do graphical formats
In MATLAB, each graph can be saved as an image file. To do that, select File (1) → Save As… (2):
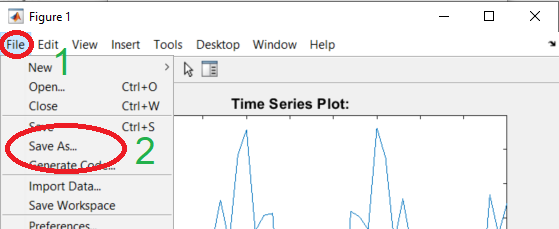
In Save As dialog you can pick from several file formats:
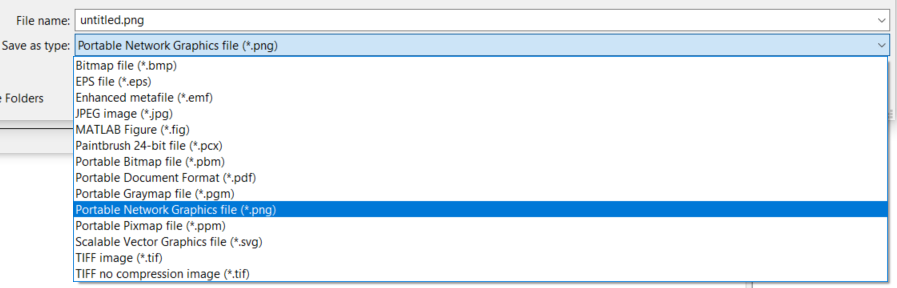
The most useful of them are:
.eps- Encapsulated Postscript - vector image format used in typesetting - pick this format if you want to embed the figure in LaTeX,.svg- Scalable Vector Graphics - universal vector format, use for example for webpage publishing,.png- Portable Network Graphics - universal lossless raster graphical format - use in scenarios, where raster images are required.
🔨 🔥 Final assignment 🔥 🔨
A CSV file containing a time vector (first column) and 5-channel electrical muscle activity (EMG) recording EMG (remaining columns): emg.csv. Download the file to the working directory of MATLAB and read into a matrix using
csvread()function.Separate the data into variables
t(time vector) andemg(values).Display all the data in a single plot Hint: by passing a matrix to
plot()fucntion, each column will be treated as a separate signal.Select the first channel. Do a simple thresholding: assign a value of 0 to all elements with value less than 40 and greater than -40. In a new window, plot the resulting vector. Hint: You can use
abs()to do only one comparison. New plotting window can be openedfigurecommand.Do the same thresholding on whole
emgmatrix. Display the data in a new figure. Remember about time values!Add description and labels to the figure:
- grid,
- title: Raw EMG data,
- x axis label: Time [s],
- y axis label: EMG [mV],
- legend: Channel 1, Channel 2…
- Save the plot in EPS format (
.eps). - Create a new LaTeX article document in TeXStudio. In the document, in a floating figure environment, embed the plot. Add a caption to the plot: Recorded EMG data
Authors: Tomasz Mańkowski, Jakub Tomczyński